4. A matter of style

Video: why style?

Imperial students can also watch this video on Panopto

4.1. The value of convention

Consider the following definition of the limit of a function \(f\) at a point \(c\):

Definition

Suppose we have a function \(f(x): \mathbb{R} \rightarrow \mathbb{R}\). Then:

\[\lim_{x\rightarrow c} f(x) = L \iff \forall\, \delta > 0,\ \exists\, \epsilon > 0,\ |x - c| < \epsilon \Rightarrow |f(x) - L| < \delta\]

This is a perfectly valid definition of a limit: you could use it to go on and derive all of real analysis. However, you would confuse yourself and your readers horribly, because I have swapped the roles of \(\delta\) and \(\epsilon\) in the definition. The formal properties of mathematical objects do not depend on the names we give them or, often, on how we lay out formulae on a page. However, mathematics is designed to be read by humans with their habit-forming, pattern-matching brains. So if everyone adopts similar conventions for how to write down mathematics, everyone schooled in those conventions will find that mathematics easier to understand. This is vitally important because understanding mathematics is hard. Non-standard notation makes it doubly hard because the reader has to consciously remember the meaning of all the symbols. Conversely, once a reader has learned the notational conventions for a field of mathematics, the meanings of the symbols become natural and don’t require conscious thought. This leaves all the available brainpower to concentrate on the mathematical content at hand.

You might at first think that this logic does not apply to computer programs. After all, a computer program is read by another computer program, and is not understood but rather acted on mechanically. Surely it doesn’t matter how it looks or what symbols you use, so long as it’s correct and, possibly, fast? This entirely understandable sentiment has afflicted almost all programmers at some point or another and typically has got them into more or less serious difficulty before they realised that it’s completely wrong.

In reality, a computer program is frequently read. Indeed, code is typically read many more times than it is written or changed. Most obviously, programmers read code in order to understand its functionality, and in order to work out what is wrong with the code when it fails to produce the correct results. Reading code is very much like reading mathematics because a computer program is nothing but a realisation of mathematical algorithms. Consequently, the observation that maths can be very hard to read carries over to code. It is therefore essential to make code as easy to understand as possible. Another analogy that carries over from mathematics is that very often it’s one’s own work that one is trying to understand and correct. This ought to create a very strong incentive to write very clear code adhering to all the conventions, because the poor individual who has to read your work to find the bugs might very well be you!

Just as in mathematics, programming has a whole set of conventions which sit on top of the formal requirements of a programming language. These exist in order to make the code easier for all programmers to read. Some of these rules, typically the more formulaic ones about matters such as code layout and naming conventions, are somewhat different in different programming languages. Others, most especially higher level principles like parsimony and modularity, are universal principles that apply more or less regardless of the language employed or the sort of programming being undertaken. Good programming style, like good writing style, is a skill learned through experience and through receiving feedback on the code you write, and it is not the intention of this chapter to produce an exhaustive guide. However, it is useful to introduce some of the key concepts, rules and conventions in a more formal way.

4.2. PEP 8

Publishers, journals, and institutions often have style guides designed to instil a certain uniformity in the use of English (or other human languages). Similarly, style guides exist for programming languages. In some languages, the preferred style can vary significantly from project to project, and there can be vigorous disagreement between factions about fine points of style, such as whether or not an opening curly bracket should start on a new line. Fortunately, the Python community has an essentially unified and very widely followed set of conventions. These are codified in one of the Python standards documents, PEP 8 [1]. PEP 8 isn’t all that long, and it is worth taking the time to read. Not every rule in PEP 8 is reproduced in this chapter, though many of the most commonly encountered ones are. Conversely, PEP 8 is rather narrowly concerned with code layout rules while this chapter roams more widely.

4.2.1. Linters

Video: installing and using a linter.

Imperial students can also watch this video on Panopto

One of the helpful characteristics of PEP 8 is that many of its strictures can be enforced automatically by a computer program. Programs that automatically check programming style are called linters. Lint are the little fibres that tend to stick to clothes, especially suit jackets, and make them ugly. So a linter is a program that finds the little ugly things in your code.

Originally, you ran the linter with your source file as an input, and it produced a report as an output, listing all of the problems it found in your code. You can still run a linter like this, and it’s very useful as an automated check that the code committed to git is clean. However, Python-aware editors are often able to run a linter for you, and display the results by highlighting code or lines of code with problem. The effect is very like the highlighting of spelling and grammar problems in many word processors and email clients.

One such program is called Flake8. Running Flake8 on all of the source code in a project, preferably automatically on every commit, is an excellent mechanism for keeping a project’s code in PEP 8 conformance. Indeed, without a mechanism like this, there is a strong tendency for programmers to cut style corners, with the effect that the code in a project becomes harder and harder to read and work with.

4.2.2. Installing Flake8

Flake8 is a Python package, which can be installed using pip. Make sure you’ve activated your virtual environment and then run:

(PoP_venv) $ python -m pip install flake8

This is enough to run Flake8 on the command line, however you will probably want to set up your editor to highlight PEP 8 incompatibilities in your source. For Visual Studio Code:

1. Install the Flake8 extension:

   1. Click the icon on the left of the screen.

   2. Type Flake8 in the search box.

   3. Click the blue Install button.

2. Instruct the extension to use Flake8 from your virtual environment:

   1. Type control + , (⌘ + , on Mac) to open the Settings tab.

   2. Type flake8.importStrategy in the Search settings bar at the top of the page.

   3. Change the dropdown from useBundled to fromEnvironment.

The video for this section shows this process.

4.2.3. How to tell Flake8 to shut up

Near the top of PEP 8 is the following heading:

A foolish consistency is the hobgoblin of little minds.

What this refers to is that just religiously following PEP 8 is not enough to produce highly readable code. Indeed, sometimes the rules might induce you do to something which makes no sense at all. In those cases, one should step outside PEP 8. This is a dangerous licence to take, and it is important to point out that this does not mean that a programmer should ignore PEP 8 merely because they disagree with a particular convention. Breaking PEP 8 is something you should do only when you really have to.

In the rare cases where it is necessary to break PEP 8, Flake8 turns into a problem. It doesn’t know anything of the judgement call that the programmer has made, and so will complain about the offending code. For example, we have learned that it is frequently desirable to import names in the __init__.py file of a package in order to include them in the package’s top level namespace. The problem with this is that these names are not used inside the __init__.py file so Flake8 will complain that this is an unnecessary import.

One way to suppress linter errors is using a special comment at the end of the line which causes the error. For example, fibonacci/__init__.py contains the following line:

from .fibonacci import fib

This causes the following Flake8 error:

$ flake8 fibonacci
fibonacci/__init__.py:1:1: F401 '.fibonacci.fib' imported but unused

We suppress this error by adding this comment:

from .fibonacci import fib  # noqa F401

The comment starts with the keyword noqa, which stands for “no questions asked” and then gives the error code which is to be ignored for this line. This can be found in the Flake8 output.

4.2.4. Configuring Flake8

noqa comments are very useful for one-off suppression of Flake8 errors. However, it’s also likely to be the case that there are some rules that you just don’t want to apply across your whole project. This configuration can be achieved in the file setup.cfg, which lives in the top of your Git repository alongside pyproject.toml. setup.cfg can be used to configure a lot of different Python tools, so it stores different configurations in different sections. Listing 4.1 shows an example Flake8 section. The full list of available options is presented in the Flake8 documentation.

Listing 4.1 A setup.cfg Flake8 section which instructs Flake8 to ignore the doc/ directory, to ignore rule D105 (docstrings for magic methods), and to add in the non-default rule W504 (error for a trailing operator at the end of a continued line).

[flake8]
exclude = doc
extend-ignore = D105
extend-select = W504

4.3. Code layout

Perhaps surprisingly, one of the most important factors in making code readable is the space, or lack of it, between and around the text which makes up the code. Whitespace affects readability in many ways. Too much code bunched together makes it hard for the eye to separate programme statements, while leaving too much space limits the amount of code which fits in the editor window at once. This requires the programmer to scroll constantly and to have to remember definitions which are not currently on the screen.

As in written prose, whitespace can also convey information by grouping together concepts which are related and separating distinct ideas. This gives the reader visual clues which can aid in understanding the code. With this in mind, we now turn to some of the PEP 8 rules around white space and code formatting.

4.3.1. Blank lines

1. Classes and functions defined at the top level of a module (i.e. not nested in other classes or functions) have two blank lines before and after them. These are the largest and most distinct units in a module, so it helps the reader to make them quite distinct from each other.

2. Methods within a class are separated by a single blank line. Similarly, functions defined inside other functions are separated from surrounding code by a single blank line.

3. Statements within functions usually follow on the immediate next line, except that logical groups of statements, can be separated by single blank lines. Think of each statement as a sentence following on from the previous, with blank lines used to divide the function into short paragraphs.

Do not add extra blank lines to space out code. Vertical space on the screen is limited, your readers will not thank you.

4.3.2. White space within lines

1. Don’t put a space after an opening bracket (of any shape), or before a closing bracket. This is because the role of brackets is to group their contents, so it’s confusing to visually separate the bracket from the contents.

   ( 1, 2) # Space after opening bracket.
   (1, 2 ) # Space before closing bracket.
   

   (1, 2) # No space between brackets and contents.
   

2. Similarly, don’t put a space between the function name and the opening round bracket of a function call, or between a variable name and the opening square bracket of an index. In each of these cases, the opening bracket belongs to the object, so it’s confusing to insert space between the object name and the bracket.

   sin (1) # Space between function name and bracket.
   x [0] # Space before index square bracket.
   

   sin(1)
   x[0]
   

3. Put a space after a comma but not before it, exactly like you would in writing prose. Following the convention that everyone is used to from writing aids understanding. Where a trailing comma comes right before a closing bracket, then don’t put a space. The rule that there are no spaces before a closing bracket is more important.

   (1,2,3) # Spaces missing after commas.
   (1 ,2 ,3) # Spurious spaces before commas.
   (1, ) # Space before closing bracket.
   

   (1, 2, 3) # Spaces after commas.
   (1,) # No space before closing bracket.
   

4. Put exactly one space on each side of an assignment (=) and an augmented assignment (+=, -=, etc.). In an assignment statement, the most important distinction is between the left and right hand sides of the assignment, so adding space here aids the reader.

   x=1 # Missing spaces around equals sign.
   x+=1 # Missing spaces around augmented addition operator.
   
   frog = 2
   cat  = 3 # Additional space before equals sign.
   

   x = 1
   x += 1
   
   frog = 2
   cat = 3
   

5. Do not put a space either before or after the equals sign of a keyword argument. In this case, grouping the parameter name and the argument is more important. This rule also creates a visual distinction between assignment statements and keyword arguments.

   myfunction(arg1 = val1, arg2 = val2)
   

   myfunction(arg1=val1, arg2=val2)
   

6. Put exactly one space before and after the lowest priority mathematical operators in an expression. This has the effect of visually separating the terms of an expression, as we conventionally do in mathematics.

   y = 3*x**2+4*x+5 # No spaces around +
   

   y = 3*x**2 + 4*x + 5
   

7. Never, ever have blank spaces at the end of a line, even a blank line. These tend to get changed by editors, which results in lots of spurious differences between otherwise identical code. This can make the difference between two commits of a file very hard to read indeed.

4.3.3. Line breaks

1. Have no lines longer than 79 characters. Limiting the line length makes lines easier to read, and prevents the editor from automatically wrapping the line in harder to read ways. Shorter lines are also very useful when using side-by-side differencing tools to show the differences between two versions of a piece of code.

2. When breaking lines to fit under 79 characters, it’s better to break the lines using the implied continuation within round, square or curly brackets than explicitly with a backslash. This is because the brackets provide good visual “book ends” for the beginning and end of the continuation. Of course this is sometimes impossible, so it is occasionally necessary to use backslashes to break lines.

3. When a mathematical operator occurs at a line break, always put the operator first on the next line, and not last on the first line. Having the second line start with a mathematical operator provides a solid visual clue that the next line is a continuation of the previous line. (If you look closely, this is also the rule that most publishers of maths books use).

   my_function(first_term + # Trailing + operator.
               second_term +
               third_term)
   

   my_function(first_term
               + second_term # Leading + operator
               + third_term)
   

4.3.4. Indentation

1. Indentation is always by four spaces per indentation level. Usually Python-aware text editors are good at enforcing this, and this is basically true of Visual Studio Code. If you’re using a text editor which doesn’t indent by four spaces (especially if it uses tab characters for indentation) then Google how to change it to four spaces!

2. When indenting continuation lines inside brackets, there are two options, usually depending on how many characters are already on the line before the opening bracket:

   1. With one or more items on the first line after the opening bracket. Subsequent lines are indented to one space more than the opening bracket, so that the first items on each line start exactly under each other. The closing bracket comes on the same line as the final item.

   capitals = {"France": "Paris",
               "China": "Beijing",
               "Australia": "Canberra"}
   

   2. With the opening bracket as the last item on the first line. Subsequent lines are indented more than the first line but the same as each other. The closing bracket comes on a new line, and is indented to the same level as the first line.

   capitals = {
       "Central African Republic": "Bangui",
       "Trinidad and Tobago": "Port of Spain",
   }
   

4.4. Names

Programs are full of names. Variables, classes, functions, modules: much, perhaps most, of the text of a program is made up of names. The choice of names, therefore, has a massive impact on the readability of a program. There are two aspects to naming conventions. One is a set of rules about the formatting of names: when to use capitals, when underscores and so on. This is covered by PEP 8 and we reproduce some of the important rules below. The second aspect is the choice of the letter, word, or words that make up a name. This is much more a matter of judgement, though there are guiding principles that greatly help with clarity.

4.4.1. PEP 8 name conventions

PEP 8 has some rather detailed rules for naming, including for advanced cases that we are unlikely to encounter in the short term, but the most important rules are short and clear:

class names

Class names use the CapWords convention: each word in a name is capitalised and words are concatenated, without underscores between.

complex_polynomial # No capitals, underscore between words.
complexPolynomial # Missing leading capital.
Complex_Polynomial # Underscore between words.

ComplexPolynomial

exception names

Exceptions are classes, so the rules for class names apply with the addition that exceptions that designate errors should end in Error.

PolynomialDivisionError # For example to indicate indivisibility.

function, variable, and module names

Almost all names other than classes are usually written in all lower case, with underscores separating words. Even proper nouns are usually spelt with lower case letters to avoid being confused with class names.

def Euler(n): # Don't capitalise function names.
MaxRadius = 10.  # No CamelCase.

def euler(n):  # Lower case, even for names.
max_radius = 10.  # Separate words with _.

method parameters

The first parameter to an instance method is the class itself. Always and without exception name this parameter self.

class MyClass:

    def __init__(instance, arg1, arg2):
    ...

class MyClass:

    def __init__(self, arg1, arg2):
    ...

non-public methods and attributes

If a method or attribute is not intended to be directly accessed from outside the class, it should have a name starting with an underscore. This provides a clear distinction between the public interface of a class and its internal implementation.

class MyClass:

    def _internal_method(self, arg1):
    ...

4.4.2. Choosing names

Short names help make short lines of code, which in turn makes it easier to read and understand what the code does to the values it is operating on. However short names can also be cryptic, making it difficult to establish what the names mean. This creates a tension: should names be short to create readable code, or long and descriptive to clarify their meaning?

A good answer to this dilemma is that local variables should have short names. These are often the most frequently occurring variables on a line of code, which makes the statement more intelligible. Should a reader be unclear what a variable stands for, the definition of a local variable will not be very far away. Conversely, a module, class, or function which might be used far from its definition had better have a descriptive name which makes its purpose immediately apparent.

4.4.3. Follow the mathematics

Remember that the key objective of code style conventions is to make it easier for readers to understand the code. If the code implements a mathematical algorithm, then it’s quite likely that readers of that code will have at least a passing acquaintance with that area of mathematics. You will therefore greatly help their intuition for what your code does if the names in the code match the mathematical conventions for the same concepts. You can use underscores to hint at subscripts, just like in LaTeX. For example, if you write a function which changes coordinates, then x_old and x_new are likely to be good names for the coordinate vector before and after the transformation.

As an exception to the rules about variable case, it is a good idea to use single capital letter names in circumstances where they would be used in the maths, for example, to name a matrix.

Mathematicians often use Greek letters as variable names, occasionally they venture further afield and use Cyrillic or Hebrew letters. Python does allow for variable names written in other alphabets, but these are hard to type on many keyboards. Someone trying to fix bugs in your code will curse you if they can’t even type the names! Do, by all means, use Greek or other language variable names where this will make the relationship between the maths and the code obvious, but write out the Greek letter name in Roman letters. For example, theta is a very good name for a variable representing an angle. Capital Greek letters are sometimes represented by capitalising the first letter of the Roman word, but take care to avoid situations where this might be confused for a class name.

4.4.4. Enforcing name conventions in Flake8

The core Flake8 package does not enforce the PEP 8 naming conventions, but there is a plugin which does so. Simply install the pep8-naming package.

$ python -m pip install pep8-naming

4.5. Parsimony

Good programming style is primarily about making programmes easy to understand. One of the key limitations of understanding is the sheer number of objects that the reader can keep in their short term memory at once. Without diverting into the psychology literature, this is only a couple of handfuls of values at most. This means that the largest amount of code that a reader can actively reason about is limited to a few operations on a few variables. As a programmer, there are two tools at your disposal to achieve this. The first is to be parsimonious and not introduce unnecessary temporary variables. The second is to use abstractions such as classes and function interfaces to split the problem up into small pieces so that each individual function or method is small enough for a reader to understand.

As a (somewhat contrived) example, assume that you need to create a list of all the positive integers less than 9999 which are divisible by all the numbers up to seven. You could write this in 5 difficult to understand lines:

result = []

for _ in range(1, 9999):
   if _ % 1 == 0 and _ % 2 == 0 and _ % 3 == 0 and _ % 4 == 0 \
       and _ % 5 == 0 and _ % 6 == 0 and _ % 7 == 0:
           result.append(_)

It would be much better to write a single more abstract but simpler line:

result = [num for num in range(1, 9999)
          if all(num % x == 0 for x in range(1, 8))]

4.5.1. Use comprehensions

It is very common to write loops to populate collection objects with values. For example, we might make a list of the first 10 square numbers for further use:

squares = []
for i in range(10):
    squares.append((i+1)**2)

This is a fairly typical, if simple, example. It takes three lines of code: one to initialise the list, one to loop, and one to add the values to the list. Alternatively, if we had used a list comprehension, all three steps would have been subsumed into a single operation:

squares = [(i+1)**2 for i in range(10)]

At least for fairly simple operations, comprehensions are almost always easier for the reader to understand than loops. In addition to lists, comprehensions are also available for sets and dictionaries.

4.5.2. Redundant logical expressions

One exceptionally common failure of parsimony is to write expressions of the following form:

if var == True:

To see the problem with this statement, let’s write out its truth table:

var	var == True
T	T
F	F

In other words, the expressions var and var == True are logically equivalent (at least assuming var is a boolean value), so it would have been more parsimonious to write:

if var:

Similarly:

if var == False:

is frowned upon by programmers in favour of:

if not var:

Finally, the use of else (or elif) can reduce the number of logical expressions that the reader has to read and understand. This means that:

if var:
    # Some code
if not var:
    # Some other code

should be avoided in favour of:

if var:
    # Some code
else:
    # Some other code.

In addition to having fewer logical operations which the reader needs to understand, the if...else version explicitly ties the two cases together as alternatives, which is an additional aid to comprehension.

4.5.3. Use the fact that every object is True or False

Every Python object is logically either True or False according to the following rules:

1. None is False.

2. Zero is False, all other numerical values are True.

3. An empty collection is False, any other container is True. For example, an empty list is False, but the list [0, 0] is True.

4. The null string "" is False, a string containing any characters is True.

5. A user-defined class is True unless:

   1. It defines the __bool__() special method. In this case the truth value is whatever this method returns.

   2. It doesn’t define __bool__() but does define __len__(). In this case the object is False if the length is zero, and True otherwise.

These rules are laid out formally in the Python documentation. One way that they can be used to write simpler, clearer code is in the very common case of code that should only execute if a collection object actually contains something. In that case, this form of test is to be preferred:

if mysequence:
    # Some code using mysequence

instead of:

if len(mysequence) > 0:
    # Some code using mysequence

4.5.4. Avoid repetition

Programmers very frequently need to do nearly the same thing over and over. One obvious way to do this is to write code for the first case, then copy and paste the code for subsequent cases, making changes as required. There are a number of significant problems with this approach. First, it multiplies the amount of code that a reader has to understand, and does so in a particularly pernicious way. A reader will effectively have to play “spot the difference” between the different code versions, and hope they don’t miss something. Second, it makes it incredibly easy for to get confused about which version of the code a programmer is supposed to be working on. There are few things more frustrating than attempting to fix a bug and repeatedly seeing that nothing changes, only to discover hours (or days) later that you have been working on the wrong piece of nearly-identical code. Finally, lets suppose that a bug is fixed - what happens to the near-identical clones of that code? The chance is very high that the bug stays unfixed in those versions thereby creating yet another spot the difference puzzle for the next person encountering a bug.

Abstractions are essentially tools for removing harmful repetition. For example, it may be possible to bundle up the repeated code in a function or class, and to encode the differences between versions in the parameters to the function or class constructor. If the differences between the versions of the code require different code, as opposed to different values of some quantities, then it may be possible to use inheritance to avoid repetition. We will return to this in Chapter 7.

4.6. Comments

Comments are non-code text included in programs to help explain what they do. Since comments exist to aid understanding, some programmers come to the conclusion that more comments imply more understanding. Indeed, some programmers are even taught that every line of code should have a comment. This could not be more wrong!

While judiciously deployed comments can be an essential aid to understanding, too many comments can be worse than too few. If the code is simple, elegant, and closely follows how a reader would expect the algorithm to be written, then it will be readily understood without comments. Conversely, attempting to rescue obscure, badly thought-through code by writing about it is unlikely to remedy the situation.

A further severe problem with comments is that they can easily become out of date. If a piece of code is modified, it is all too easy for the programmer to neglect to update accompanying comments. The result is comments which explain one thing, code which does something else, and exceptionally baffled readers.

4.6.1. Three rules for commenting

1. If code is so simple, clear, and obvious that it can be easily understood without comments, don’t comment.

2. If code is not easily understood without comments, the problem is probably the code. Refactor the code to be simpler and easier to understand.

3. If, and only if, you are convinced that it is strictly necessary to do something unobvious, then do so and include a comment.

4.6.2. Comment why, not what

Even where a comment is unavoidable, it should still usually be obvious what it is that code does. It is far more likely to be justifiable to include a comment about why a particular approach is taken. For example, it might be worth commenting why an apparently simpler alternative strategy is actually invalid.

4.6.3. PEP 8 rules for comments

Comments start with a single # followed by a single space. Inline comments are separated from the code by at least two spaces.

self.count += 1# No space between code and comment.

self.count += 1  #No space between # and comment text.

self.count += 1  # Two spaces before #, one after.

Each line of a block comment starts with a single # indented to the same level as a normal line of code. The # is followed by a single space, unless a particular piece of comment should be indented with respect to the paragraph it is in, in which case additional spaces are allowed.

if somecondition(data):
    # Comment indented to the same level as the contents of the if
    # block.

4.7. Docstrings

There is one enormous exception to the rule that comments should be used only sparingly: docstrings. Docstrings (a portmanteau of “documentation strings”) are comments at the start of modules, classes, and functions which describe public interfaces. The entire point of a public interface is that the programmer using it should not have to concern themselves with how it is implemented. They should, therefore, not need to read the code in order to understand how to use it.

The Python interpreter has special support for docstrings. When a user calls help() on an object (including a function or method) then any docstring on that object is used as the body of the resulting help message. Docstrings are also understood by the Python documentation generation system, Sphinx. This enables documentation webpages to be automatically generated from Python code. The Python documentation in this course is generated by this system. For example, recall that we met the function fib(), which calculates Fibonacci numbers, in Section 2.3. We can ask fib() for its documentation:

In [1]: import fibonacci
In [2]: help(fibonacci.fib)

The following is displayed:

Help on function fib in module fibonacci.fibonacci:

fib(n)

Return the n-th Fibonacci number.

There is also a specific IPython help extension, which also works in Jupyter notebooks (IPython and Jupyter are related projects). Appending a question mark ? to an object name prints a slightly different version of the help information:

In [3]: fibonacci.fib?
Signature: fibonacci.fib(n)
Docstring: Return the n-th Fibonacci number.
File:      ~/docs/principles_of_programming/object-oriented-programming/fibonacci/fibonacci.py
Type:      function

Finally, the same information is used in the web documentation. Notice that the function signature is not a part of the docstring. Python is capable of extracting the signature of the function and adding it into the documentation without the programmer having to manually add it to the docstring.

4.7.1. Where to use docstrings

Every public module, class, function, and method should have a docstring. “Public” in this context means any code which is intended to be accessed from outside the module in which it is defined.

4.7.2. Docstring conventions

Python itself doesn’t know anything about docstring contents, it will simply display the docstring when you ask for help. However, other tools such as those that generate websites from documentation depend on you following the conventions.

By convention, docstrings are delimited by three double quote characters (""").

4.7.3. Short docstrings

Simple functions which take one or two arguments can be documented with a single line docstring which simply says what the function does. The Fibonacci example above is a typical case. The single line should be an imperative sentence and end with a full stop.

def fib(n):
    "Return the n-th Fibonacci number"  # Single quotes,
                                        # no full stop.

def fib(n):
    """Returns the n-th Fibonacci number."""  # Sentence not
                                              # imperative.

def fib(n):
    """fib(n)
    Return the n-th Fibonacci number."""  # Don't include the
                                          # function signature.

def fib(n):
    """Return the n-th Fibonacci number."""

4.7.4. Long docstrings

Conversely, a more complex object will require much more information in its docstring. Listing 4.2 shows the full docstring of the function numpy.linalg.det(). This covers the type and shape of the input parameter and return value, references to other implementations, and examples of usage.

There is no single universal standard for the layout of a long docstring, but there are two project or institution-based conventions that are recognised by the web documentation system. One from Google and the other from the Numpy project. You should consistently use one of these styles across a whole project. Clearly if you are contributing code to an existing project then you should follow their style.

Listing 4.2 The docstring for numpy.linalg.det(). This is a long docstring using the Numpy convention.

def det(a):
    """
    Compute the determinant of an array.

    Parameters
    ----------
    a : (..., M, M) array_like
        Input array to compute determinants for.

    Returns
    -------
    det : (...) array_like
        Determinant of `a`.

    See Also
    --------
    slogdet : Another way to represent the determinant, more suitable
      for large matrices where underflow/overflow may occur.
    scipy.linalg.det : Similar function in SciPy.

    Notes
    -----
    .. versionadded:: 1.8.0
    Broadcasting rules apply, see the `numpy.linalg` documentation for
    details.
    The determinant is computed via LU factorization using the LAPACK
    routine ``z/dgetrf``.

    Examples
    --------
    The determinant of a 2-D array [[a, b], [c, d]] is ad - bc:
    >>> a = np.array([[1, 2], [3, 4]])
    >>> np.linalg.det(a)
    -2.0 # may vary
    Computing determinants for a stack of matrices:
    >>> a = np.array([ [[1, 2], [3, 4]], [[1, 2], [2, 1]], [[1, 3], [3, 1]] ])
    >>> a.shape
    (3, 2, 2)
    >>> np.linalg.det(a)
    array([-2., -3., -8.])
    """

4.7.5. Enforcing docstring conventions in Flake8

The core Flake8 package does not enforce docstring conventions, but there is an additional package flake8-docstrings which will do this for you. This is installed using:

$ python -m pip install flake8-docstrings

Because there is more than one convention for long docstrings, this package needs a little bit of configuration. You can select the docstring convention on the command line:

$ flake8 --docstring-convention numpy

or by saving the configuration option in a config file. For example you can add a file setup.cfg alongside pyproject.toml at the top of your git repository, and include the following:

[flake8]
docstring-convention=numpy

Alternative specifications for docstring conventions that are supported are google and pep257.

4.8. A brief diversion into cellular automata

We’ll now take a brief diversion into a completely different area of mathematics: cellular automata. This is entirely irrelevant to the subject at hand, except that it provides a useful and, hopefully, interesting basis for this chapter’s exercises. The Game of Life is a mathematical system invented by the mathematician John Horton Conway FRS in 1970. The board of the game is a grid of squares, like an infinite piece of graph paper (though we’ll only work with finite boards, since our computers have finite memory). Each cell on the board is either alive (value 1) or dead (value 0). The only human interaction is to set the initial state of every square on the board to either alive or dead. The game then proceeds as a series of steps. At each step the new state of the board is calculated according to these rules:

1. The neighbours of a square are the 8 immediately surrounding squares.

2. Any square with exactly 3 live neighbours at the old step is live at the new step.

3. Any square which is alive at the old step and has exactly 2 live neighbours at the old step remains alive at the new step.

4. All other squares on the board at the new step are dead.

Using only these three rules, an amazingly complex array of behaviour can be generated, depending only on the pattern of cells which starts off alive. For example there are patterns of cells which are fixed, called “rocks”, “gliders” that fly across the board and “oscillators” which repeatedly switch between a few states. It’s simultaneously a fun toy and an important piece of mathematics. For example, it’s possible to prove that any algorithm that can be executed on any computer can be represented by a suitable pattern of game of life cells, and running the game will execute the algorithm.

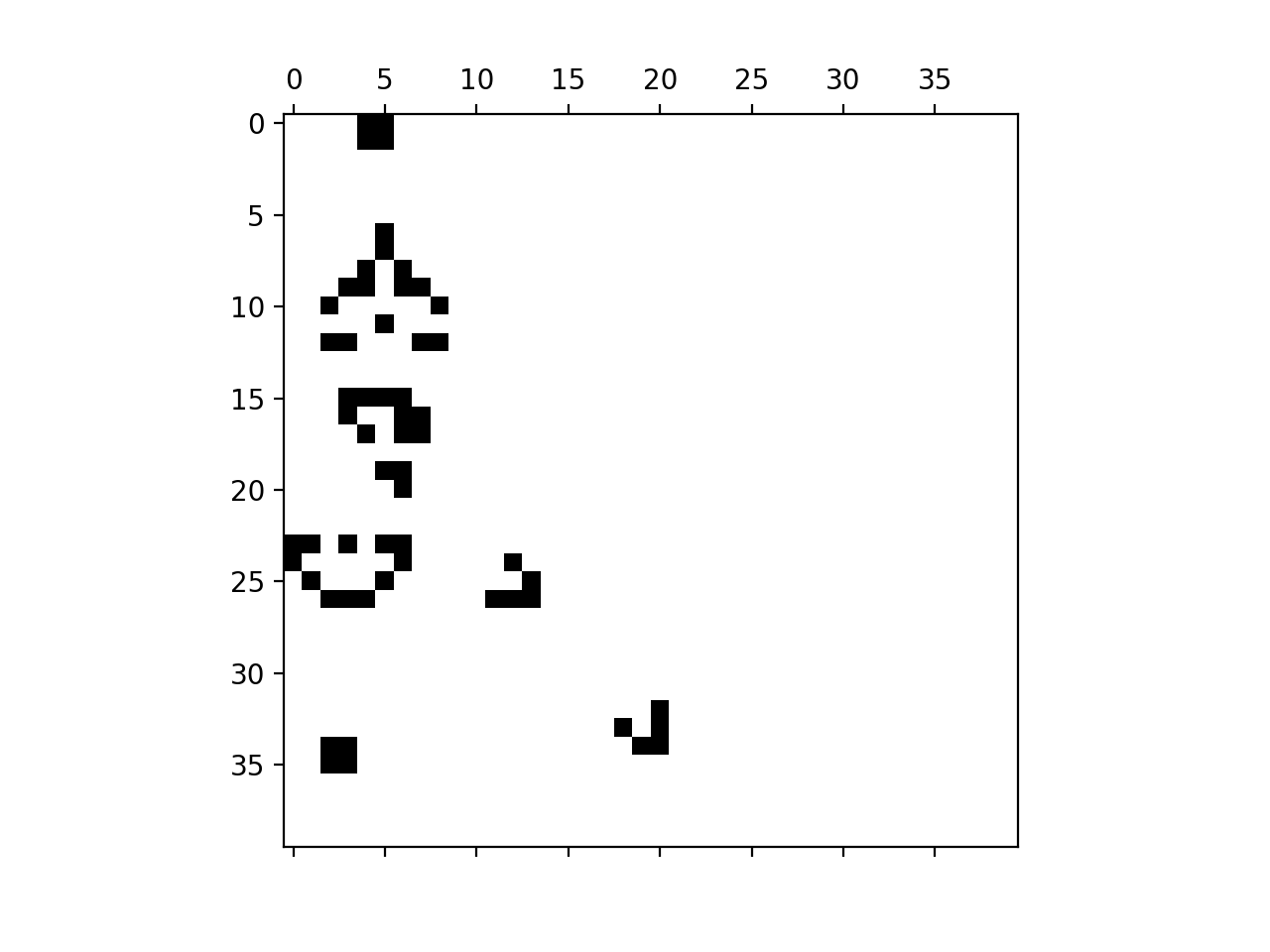
Fig. 4.1 Snapshot of the Game of Life at one step. The black squares are live and the white ones are dead. Two gliders can be seen moving across the board at (25, 12) and (33, 19).

4.9. Glossary

block comment

A comment which is the only text on one or more lines of code. Block comments are typically used to describe the code that follows them.

docstring

A literal string included at the start of a module, class or function which documents that code object.

function signature

The signature of a function is the name of the function and the arguments that it takes. The function signature is the basic information needed in order to know how to call that function.

inline comment

A comment which follows active code on a line. Inline comments are used to make a very brief clarification of the code on that line.

modularity

The design principle that programs should be broken into small, easily understandable units, which communicate with each other through clearly specified interfaces.

parsimony

The design principle that unnecessary code, names, and objects should be avoided.

4.10. Exercises

Exercise

Install flake8, pep8-naming, and flake8-docstrings. Configure your Python editor to use flake8.

The skeleton code on GitHub for this chapter’s exercises contains a package life which implements Conway’s Game of Life. Using the information on the book website obtain the skeleton code for these exercises. Clone the repository into your working folder and install the package in editable mode.

A couple of example scripts are provided which demonstrate the game of life. This one shows a glider flying across the board:

$ python scripts/glider.py

Running the script will pop up a window showing the board. If Visual Studio Code is in full screen mode then that pop-up might appear on a different screen. It’s therefore a good idea to unmaximise Visual Studio Code before running the script.

This script shows a glider gun, which generates a neverending sequence of gliders:

$ python scripts/glider_gun.py

Exercise

The author of the life package had clearly never heard of PEP 8: the style of the code is awful. Fix the style in the package so that there are no Flake8 errors. Among other things, you will need to write docstrings for all of the methods. The configuration file in the skeleton code sets the convention to Numpy, but actually you should only need short docstrings in this case so this won’t make a difference.

Exercise

Fig. 4.2 From left to right: an upright glider, a vertically flipped glider, a horizontally flipped glider, and a transposed glider.

A pattern such as a glider maintains its behaviour if translated, reflected or rotated.

1. Add a class Pattern to life.life. The constructor should take in a numpy array containing a pattern of 1s and 0s, and assign it to the attribute grid.

2. Add Pattern to the import statement in life.__init__.

3. Add a method flip_vertical() which returns a new Pattern whose rows are in reversed order, so that the pattern is upside down.

   Hint

   A slice of the form ::-1 returns that dimension of an array in reverse order.

4. Add a method flip_horizontal() which returns a new Pattern whose rows are in reversed order, so that the pattern is reversed left-right.

5. Add a method flip_diag() which returns a new pattern which is the transpose of the original.

6. Add a method rotate() with a parameter n. This should return a new Pattern which is the original pattern rotated through n right angles anticlockwise.

   Hint

   A rotation is the composition of a transpose and a reflection.

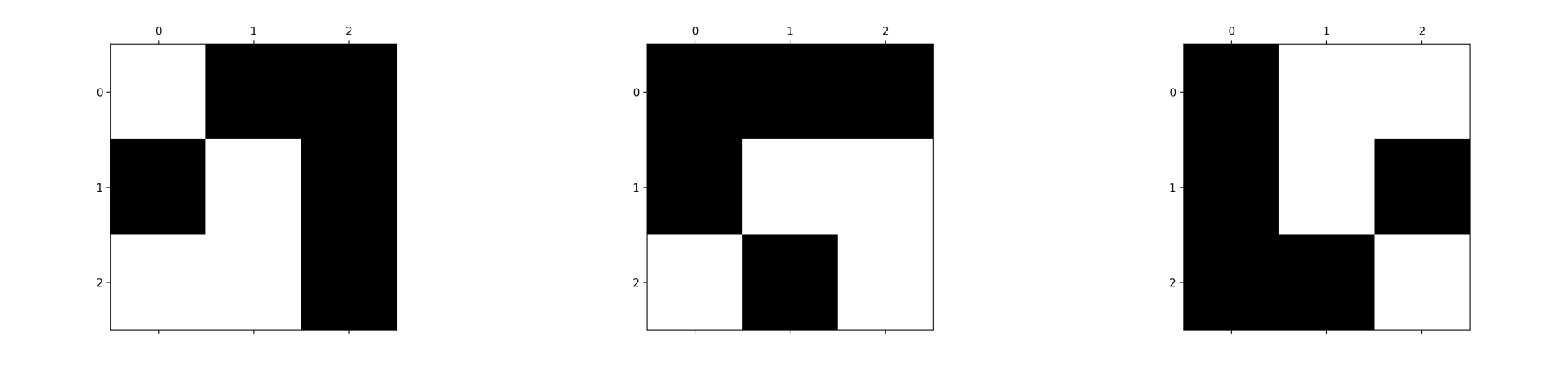
Fig. 4.3 Gliders rotated by 1, 2, and 3 right angles anticlockwise.

Exercise

Add a method insert() to the Game class. This should take two parameters, a Pattern and a pair of integers representing a square on the game board. The method should modify the game board so as to insert the pattern provided at a location centred on the location given by the pair of integers. Fig. 4.4 illustrates this operation.

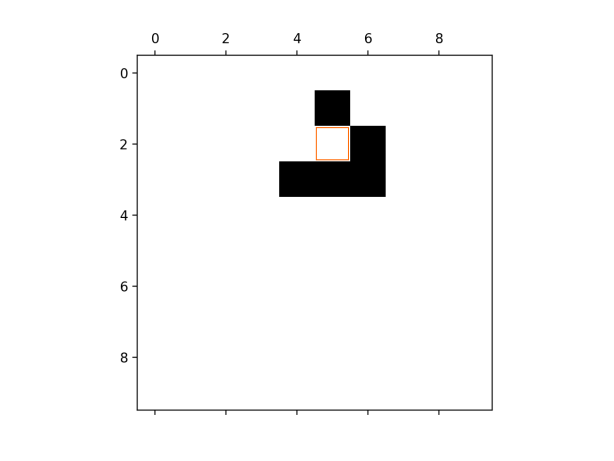
Fig. 4.4 A glider inserted at the location (2, 5). The insertion location is highlighted in orange.

Once you have completed the exercises, the third script provided will work. This sets up two gliders which collide and eventually turn into a pattern of six oscillating blinkers:

$ python scripts/two_gliders.py

Footnotes

[1]

PEP stands for “Python Enhancement Proposal”. PEPs describe everything from code style to voting algorithms among Python developers. Their main purpose, as the name suggests, is to document proposals for changes to the Python language. As such, they are usually of little interest to most Python users. However the PEPs having to do with style have wider significance.

[2]

https://object-oriented-python.github.io/edition3/exercises.html